Question
If you have a line of unit length and take two cuts, each independently and uniformly distributed over the line’s length, what is the probability that the resulting segments makes a triangle?
When do three segments make a triangle?
Well, the classic triangle inequality shows that: $$||x + y|| \leq ||x|| + ||y||$$ That is, the sum of the lengths of two sides, must be greater than the length of the remaining side. For this application, this means that a triangle emerges if and only if the longest segment is less than $\frac{1}{2}$.
Take $(x_{1}, x_{2})$ to be the lengths of the cuts measured from the “left” of the line segment.
In the case where $x_{1} < x_{2}$, then to make a triangle, we require: $$x_{1} < \frac{1}{2}$$ $$x_{2} < x_{1} + \frac{1}{2}$$ And similarly, but symmetrically, for $x_{2} < x_{1}$

Graphically, we can see the regions where $(x_{1}, x_{2})$ form a triangle with these constraints below:
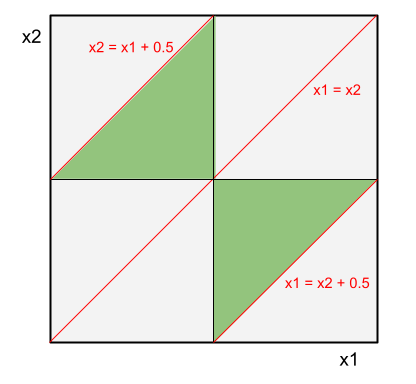
Working this out rigourously, the probability of making a triangle is: $$P(\text{Triangle}) = P(x_{1} < x_{2}) P\left(x_{1} < \frac{1}{2},x_{1} < x_{2} < x_{1} + \frac{1}{2}\right) + P(x_{2} < x_{1}) P\left(x_{2} < \frac{1}{2}, x_{2} < x_{1} < x_{2} + \frac{1}{2}\right) $$ $$P(\text{Triangle}) = \frac{1}{2}\int_{0}^{\frac{1}{2}}\int_{x_{1}}^{x_{1}+\frac{1}{2}}1 dx_{2}dx_{1} + \frac{1}{2}\int_{0}^{\frac{1}{2}}\int_{x_{2}}^{x_{2}+\frac{1}{2}}1 dx_{1}dx_{2}$$ $$P(\text{Triangle}) = \int_{0}^{\frac{1}{2}}\frac{1}{2} dx_{1} \text{ by symmetry}$$ $$P(\text{Triangle}) = \frac{1}{4}$$
Extension 1
What is the probability you make an equilateral, isosceles or scalene triangle? With two random cuts, there are two ways to make an equilateral triangle - which have zero probability measure: $$P(\text{Equilateral}) = P\left(x_{1} = \frac{1}{3}, x_{2} = \frac{2}{3}\right) + P\left(x_{2} = \frac{1}{3}, x_{1} = \frac{2}{3}\right) = 0$$
There are an infinity of ways to make an isosceles triangle with two random cuts. For the case where $x_{1} < x_{2}$, we see below that for any given $x_{1}$, there are three possible $x_{2}$ cuts that would result in an isosceles:
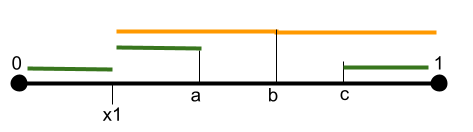
However, the probability of having the segments result in an isosceles triangle remains zero: $$P(\text{Isosceles}) = \frac{1}{2}P(x_{2} \in {a, b, c} | x_{1} < 0.5 ) + \frac{1}{2}P(x_{1} \in {} | x_{2} < 0.5 )$$ $$P(\text{Isosceles}) = P(x_{2} \in {a, b, c}) \text{ by symmetry, Bayes and independence}$$ $$P(\text{Isosceles}) = 0$$
Resultingly, making two random cuts that forms a a triangle, has a probability of 1 of being a scalene triangle!
Extension 2
If you make $n-1$ cuts, what is the probability the segments make an $n$-gon? Extending the triangle inequality, we see that, to make an $n$-gon, the longest side must be less than $\frac{1}{2}$.
For each segment, the probability that it is longer than $\frac{1}{2}$ is $P\left(\min_{i} x_{i} > \frac{1}{2}\right) = \left(\frac{1}{2}\right)^{n-1}$. For $n$ segments, the probability that we don’t make an $n$-gon is then $\frac{n}{2^{n-1}}$.
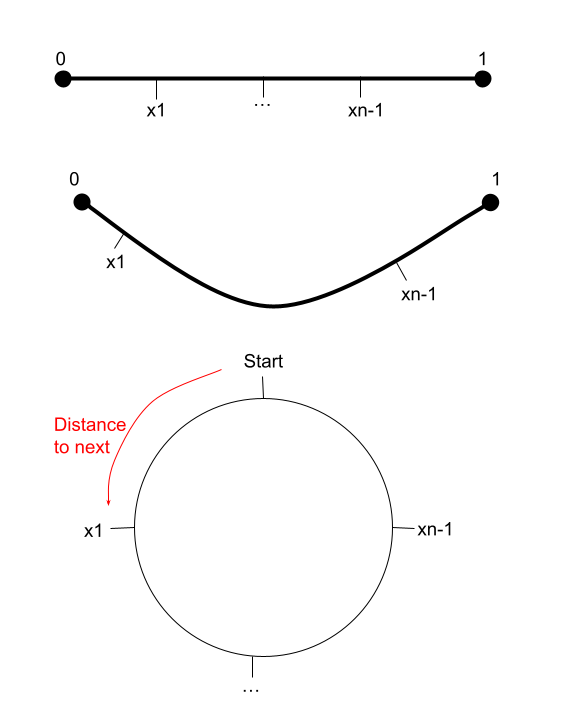
So then, the probability that we make an $n$-gon is: $$P(n\text{-gon}) = 1 - \frac{n}{2^{n-1}}$$